Bài viết này sẽ hướng dẫn tất tần tật cách tính toán diện tích mặt cầu và thể tích của hình cầu. Hãy cùng theo dõi ngay bên dưới cùng upes2.edu.vn Việt Nam.
Đang xem: Công thức tính diện tích hình cầu
Định nghĩa mặt cầu, khối cầuCách tính diện tích mặt cầu ngoại tiếp hình chópCách tính diện tích mặt cầu ngoại tiếp hình lập phương và mặt cầu nội tiếp hình lập phương
Định nghĩa mặt cầu, khối cầu
Định nghĩa mặt cầu
Cho điểm I cố định và một số thực dương r
Tập hợp tất cả các điểm M nằm trong không gian cách I một khoảng bằng r được gọi là mặt cầu tâm I bán kính r.
Kí hiệu mặt cầu: S (I; r) = {M|IM=r}
Khối cầu hay hình cầu là gì ?
Khối cầu (Hình cầu) tâm I bán kính r là tập hợp các điểm thuộc mặt cầu S (I; r) và các điểm nằm trong mặt cầu đó
Công thức tính diện tích mặt cầu và thể tích khối cầu bán kính r, tâm I
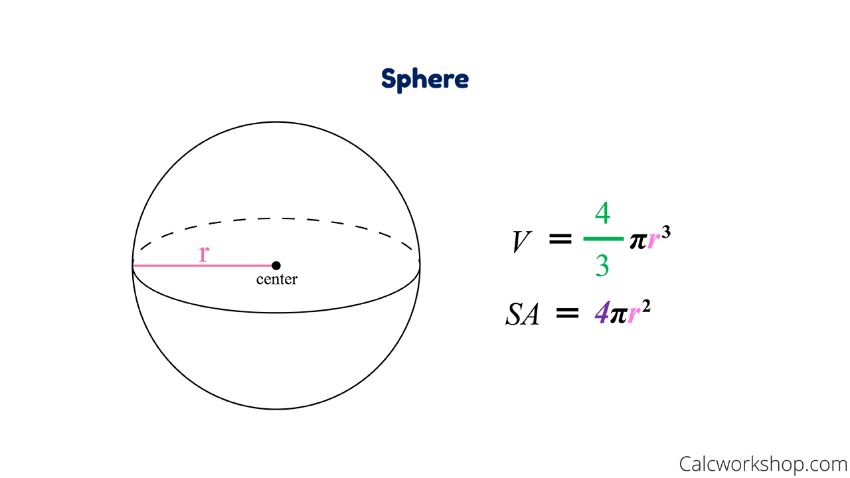
Công thức tính diện tích mặt cầu S (I; r)
S = 4 π r2
Trong đó:
S là diện tích mặt cầu tâm I bán kính r
r là bán kính hình cầu
Công thức tính thể tích hình cầu S (I; R)
V = 4/3 π r3
Trong đó
V là thể tích mặt cầu tâm I bán kính r
R là bán kính mặt cầu tâm I
Cách tính diện tích mặt cầu ngoại tiếp hình chóp
Mặt cầu ngoại tiếp hình chóp nếu nó đi qua mọi đỉnh của hình chóp. Để tính diện tích mặt cầu ngoại tiếp hình chóp, chúng ta cần xác định tâm của mặt cầu ngoại tiếp. Ngoài ra có thể áp dụng phương pháp tính nhanh với một số dạng toán cụ thể.
Phương pháp xác định tâm mặt cầu ngoại tiếp hình chóp
Bước 1: Xác định trục của đường tròn ngoại tiếp đa giác đáy, là đường thẳng vuông góc với đáy tại tâm đường tròn ngoại tiếp đa giác đáy.
Bước 2: Xác định mặt phẳng trung trực của một cạnh bên. Hoặc trục của đường tròn ngoại tiếp mặt bên.
Xem thêm: Cách Search Tìm Kiếm Và Thay Thế Trong Word, Đơn Giản Cách Tìm Và Thay Thế Trong Word
Bước 3: Giao điểm của trục của đáy và mặt phẳng trung trực của một cạnh bên (hoặc trục của đường tròn ngoại tiếp mặt bên) là tâm mặt cầu ngoại tiếp hình chóp.
Trong một vài trường hợp đặc biệt, có thể có công thức tính nhanh diện tích mặt cầu ngoại tiếp hình chóp
Trường hợp 1: Hình chóp có các đỉnh cùng nhìn 1 cạnh AB góc 90 độ
Các đỉnh này không nằm trên cạnh đó) dưới góc 90 độ, bán kính đường tròn ngoại tiếp hình chóp đó: R=AB/2 , diện tích mặt cầu ngoại tiếp hình chóp S= 2 π AB2
Ví dụ: Cho hình chóp S.ABC, đáy là hình tam giác ABC có góc B bằng 90 độ, cạnh SA vuông góc với đáy tại điểm A. Tính diện tích mặt cầu ngoại tiếp hình chóp S.ABC biết SC = 2a
=> Bán kính mặt cầu ngoại tiếp hình chóp SABC: r = SC/2 = a
=> Diện tích mặt cầu ngoại tiếp hình chóp S.ABC: S= 4 π a2
=> Thể tích khối cầu ngoại tiếp hình chóp SABC: V = 4/3 π r3
Trường hợp 2: Mặt cầu ngoại tiếp hình chóp tam giác đều SABC, SA = a
Bán kính mặt cầu ngoại tiếp hình chóp SABC: r = SA2 /2.SO
Diện tích mặt cầu ngoại tiếp hình chóp SABC: S= 4 π R2 = 3/2 π a2
Trường hợp 3: Diện tích mặt cầu ngoại tiếp hình chóp tứ giác đều đáy SABCD,
Hình chóp tứ diện đều có ABCD là hình vuông. O là tâm hình vuông ABCD đồng thời là tâm mặt cầu ngoại tiếp hình chóp SABCD.
=> Bán kính mặt cầu ngoại tiếp hình chóp SABCD: r = OD
Ví dụ: Cho hình chóp S ABCD là hình chóp tứ giác đều có tất cả các cạnh bằng a. Tính diện tích mặt cầu ngoại tiếp hình chóp SABCD
Bán kính mặt cầu ngoại tiếp hình chóp SABCD
R= OD = (a √ 2)/2
Diện tích mặt cầu ngoại tiếp hình chóp tứ diện đều SABCD
S = 4 π R2 = 2 π a2
Cách tính diện tích mặt cầu ngoại tiếp hình lập phương và mặt cầu nội tiếp hình lập phương
Hình lập phương có cả mặt cầu ngoại tiếp và mặt cầu nội tiếp.
Xem thêm: Tin Nhắn Chúc Buổi Sáng Cho Bạn Gái, Những Lời Chúc Buổi Sáng Ngọt Ngào, Yêu Thương
Diện tích mặt cầu ngoại tiếp hình lập phương
Bán kính mặt cầu ngoại tiếp hình lập phương cạnh a: r = (a √ 3)/2
Diện tích mặt cầu ngoại tiếp hình lập phương cạnh a: S = 3 π a2
Thể tích mặt cầu ngoại tiếp hình lập phương cạnh a: V =√ 3 /2 π a3
Diện tích mặt cầu nội tiếp hình lập phương
Bán kính mặt cầu ngoại tiếp hình lập phương cạnh a: r = a/2
Diện tích mặt cầu ngoại tiếp hình lập phương cạnh a: S = π a2
Thể tích mặt cầu ngoại tiếp hình lập phương cạnh a: V = ⅙ π a3
Cách tính diện tích mặt cầu ngoại tiếp hình hộp chữ nhật
Cho hình hộp chữ nhật ABCD A”B”C”D’ có độ dài các cạnh lần lượt là a,b,h
Bán kính mặt cầu ngoại tiếp hình hộp chữ nhật: R= (√ (a2 +b2 +h2) )/2
Diện tích mặt cầu ngoại tiếp hình hộp chữ nhật : S = π (a2 +b2 +h2)
Cách tính diện tích mặt cầu ngoại tiếp hình lăng trụ tam giác đều
Cho hình lăng trụ tam giác đều ABC A”B”C’ có độ dài cạnh đáy = chiều cao =a
Gọi O và O’ lần lượt là trọng tâm của 2 đáy tam giác ABC và A’BC’
=> Trung điểm I của đoạn OO’ là trọng tâm của mặt cầu ngoại tiếp hình lăng trụ tam giác đều ABC A”B”C’
Bán kính mặt cầu ngoại tiếp hình lăng trụ tam giác đều:
R = IC = √(IO’2 +O’C;2) = ( a√21 )/6
Diện tích mặt cầu ngoại tiếp hình lăng trụ tam giác đều
S = 4 π R2 = 7/3πa2
Tổng kết công thức tính diện tích mặt cầu như sau
|
Dạng bài tính diện tích mặt cầu |
Công thức |
|
Diện tích mặt cầu S(I;r) |
S = 4 π r2 |
|
Thể tích mặt cầu S (I;r) |
V = 4/3 π r3 |
|
Diện tích mặt cầu ngoại tiếp hình chóp có các đỉnh nhìn cạnh AB 1 góc 90 độ có SA = 2a |
S= 4 π a2 |
|
Diện tích mặt cầu ngoại tiếp hình chóp tam giác đều SABC có SA = a |
S = 3/2 π a2 |
|
Diện tích mặt cầu ngoại tiếp hình chóp tứ giác đều S ABCD có SA =a |
S = 2 π a2 |
|
Diện tích mặt cầu ngoại tiếp hình lập phương cạnh a |
S = 3 π a2 |
|
Diện tích mặt cầu nội tiếp hình lập phương cạnh a |
S = π a2 |
|
Cách tính diện tích mặt cầu ngoại tiếp hình hộp chữ nhật |
S = π (a2 +b2 +h2) |
|
Cách tính diện tích mặt cầu ngoại tiếp hình lăng trụ tam giác đều |
S = 7/3πa2 |
Bài tập vận dụng công thức tính diện tích mặt cầu
Cho hình chóp tam giác S ABC nội tiếp đường tròn, các cạnh SA, SB, SC đôi một vuông góc với nhau và có kích thước lần lượt là: a,b,c. Tính diện tích mặt cầu và thể tích khối cầu ngoại tiếp hình chóp SABC
Cách giải chi tiết
Gọi M là trung điểm của cạnh AB
=> Tam giác SAB là tam giác vuông tại S
=> SM = MA=MB = ½ AB (SM là đường trung tuyến)
=> M là tâm đường tròn ngoại tiếp tam giác SAB
Kẻ đường thẳng α qua M và vuông góc với mặt phẳng (SAB)
Trong mặt phẳng tạo bởi α và SC, đường trung trực của SC cắt α tại điểm I
=> IS = IC (1)
Mà IS = IA = IB (2)
Suy ra IA=IB=IC=IS
=> I là tâm đường tròn ngoại tiếp hình chóp SABC, bán kính IS=IA=IB=IC
Ta có:
SM = ½ AB = ½ √ (SA2 +SB2 ) = ½ √ (a2 +b2 )
IM = SC/2 = c/2
Bán kính R = IS = 1/2AB = 1/2√ (a2 +b2 +h2 )
Diện tích mặt cầu ngoại tiếp hình chóp SABC là
S = 4 π R2 = (a2 +b2 +c2)π
Thể tích mặt cầu ngoại tiếp hình chóp SABC là
V = 4/3 π R3 = ⅙ π (a2 +b2 +c2)3/2
Để tính diện tích mặt cầu S tâm I bán kính R ký hiệu (I;R), và thể tích khối cầu (hình cầu) V tâm I bán kính R ký hiệu (I;R) chúng ta chỉ việc áp dụng công thức sau khi tính được bán kính mặt cầu,
Tuy nhiên, việc xác định tâm của mặt cầu và bán kính của mặt cầu là không dễ và cần vận dụng qua nhiều bài học để tư duy tốt hơn trong các phương pháp tính. Ngoài ra, cần có kiến thức tổng hợp về hình học để có thể thành công với đa dạng bài tập.
Hy vọng sau bài viết hôm nay, các bạn đã có được kiến thức hữu ích để tính diện tích mặt cầu và thể tích hình cầu. Chúc các bạn thành công!